行星形变理论（1）

啊……

牛顿曾经说过，球对称行星对球外一点的引力等价于其所有质量集中于球心，因为基本上所有天体都是球，所以它们之间的作用大概就是简单的二次反比力。

但这样就完了岂不是很没有逼格……于是就有了这篇文章。

写了写，感觉全塞一篇里太长了，所以分成几个部分。第一部分讨论天体因自转和潮汐作用产生的形变，以及因这形变产生的额外引力势。

天坑预感……不知道什么时候能写完……

警告：文中有很多很长的公式。很长是多长呢？

一一一一一一一一一一一一一一一一我是很长的公式一一一一一一一一一一一一一一一一一

大概有这么长。如果上面一行被换行了，说明显示器宽度不够，可以试试调低缩放比例，或者手机横屏什么的……

第一章 高中物理学：行星因自转或潮汐产生的扁率

考虑一个质量为\(M\)，半径为\(R\)的球体行星（如下图虚线）。给它一个自转角速度\(\omega\)，使得它产生形变（如下图实线）。

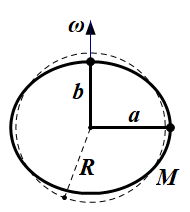
首先假设此时行星的引力仍然等价于质点引力\(\vec g=-GM\vec r/r^3\)。

再假设形变之后是一个椭球，其赤道半径（长轴）为\(a\)，极半径（短轴）为\(b\)。至于为什么是个椭球，都是细节不要在意……其实严格的等势面并不是椭球，但可以用一个椭球来进行一阶近似，而且这样做相当方便。也就是说不做这个近似就没法玩了……

写出赤道和极点的等势方程\[-\frac{GM}{a}-\frac{1}{2}\omega^2a^2=-\frac{GM}{b}\]

注意我们有一阶近似，也就是说假设扁率是个小量，\(a\)、\(b\)和\(R\)差得不多：\[\frac{1}{2}\omega^2a^2=\frac{GM}{b}-\frac{GM}{a}\approx -\frac{GM}{R^2}(b-a)\]

可以直接算出扁率\[f_\omega=\frac{a-b}{a}=\frac{\omega^2R^3}{2GM}\]

很好。这就是高中物理告诉我们的自转引起的行星扁率。

接下来继续计算潮汐作用：

仍然考虑那个质量为\(M\)，半径为\(R\)的球体行星。这次不给它角速度了，而是在它旁边距离为\(r\)（从行星中心算起）的地方放置一个质量为\(m\)的质点，给它一个潮汐力使得它形变。

首先说明什么是潮汐力，如图：

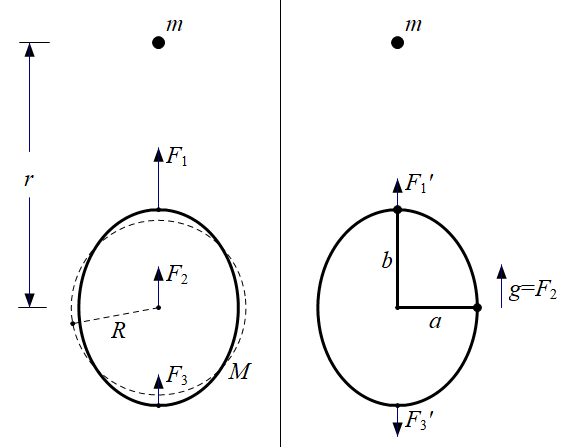
\(m\)在\(M\)各处分别造成引力\(\vec F_1\)，\(\vec F_2\)和\(\vec F_3\)，平均起来大概是\(\vec g=\vec F_2=Gm\vec r/r^3\)。这个平均引力使整个\(M\)具有加速度\(\vec g\)，于是\(M\)参考系中就有一个等效的惯性力\(-\vec g\)，潮汐力就是\(m\)的引力被这个惯性力\(-\vec g\)抵消后剩下的力。

在潮汐力作用下，行星形变之后仍然假设其是一个椭球，赤道半径为\(a\)，极半径为\(b\)。注意现在赤道半径是短轴，极半径是长轴，和刚刚讨论自转时刚好相反。这是为了保证无论何种情况下，行星都拥有关于极轴的轴对称性，也就是说行星椭球总是\(a\times a\times b\)的。

仍然写出赤道和极点的等势方程
\[-\frac{GM}{a}-\frac{Gm}{\sqrt{r^2+a^2}}=-\frac{GM}{b}-\frac{Gm}{r-b}+b\cdot\frac{Gm}{r^2}\]

移项
\[\frac{GM}{b}-\frac{GM}{a}=\left(\frac{Gm}{\sqrt{r^2+a^2}}-\frac{Gm}{r-b}\right)+b\cdot\frac{Gm}{r^2}\]

等式左侧取一阶近似，\(a\approx b\approx R\)；对等式右侧，假设\(a\)，\(b \ll r\)，将括号里的算式展开到二阶小量（第一阶被等效惯性力引起的势能项消掉了）
\[-\frac{GM}{R^2}(b-a)=\left(-\frac{Gm}{r^2}\cdot b-\frac{Gm}{r^3}\cdot b^2-\frac{Gm}{2r^3}\cdot a^2\right)+b\cdot\frac{Gm}{r^2}\]

整理可得扁率
\[f_m=\frac{a-b}{a}=-\frac{3GmR^3}{2GMr^3}\]

完毕。这就是高中物理计算出来的潮汐力造成的行星扁率。这个扁率是负的，因为潮汐力把行星拉成了一个长椭球（而自转会把行星压成扁椭球，具有正的扁率）。

第二章 形变的矩阵表示与叠加

刚刚我们分别对自转和潮汐影响算出了行星扁率，但只有一个扁率是不够的。实际中的行星不光有自转，同时还受到不止一个别的行星对它造成的潮汐影响。这一章讨论这些形变如何表示与叠加。

还是考虑质量为\(M\)，半径为\(R\)的球体行星。如果它受到某种作用变成了赤道半径为\(a\)，极半径为\(b\)的椭球体，那么取其极轴为\(z\)轴建立坐标系，可以写出变换矩阵
\[T=
\begin{pmatrix}
a/R & 0 & 0 \\
0 & a/R & 0 \\
0 & 0 & b/R
\end{pmatrix}\]

显然，如果\(P\)是半径为\(R\)的球体行星上一点，那么\(TP\)就是它在变形后的椭球体行星上对应的点。

如果要求变形过程行星的体积（或密度）不变，而且要求扁率为\(f\)，则可以写出关于\(a\)和\(b\)的方程：
\[a^2b=R^3, \frac{a-b}{a}=f\]

解得\(a/R=(1-f)^{-1/3}\)，\(b/R=(1-f)^{2/3}\)。

当\(f\)是小量时，有\(a/R\approx 1+f/3\)，\(b/R\approx 1-2f/3\)。此时定义\(C=T-I\)，则
\[C=
\frac{1}{3}\begin{pmatrix}
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & -2f
\end{pmatrix}=\left(\frac{I}{3}-\hat z\hat z\right)f\]

注意到\(C\)与扁率\(f\)是同阶小量。称这个\(C\)为形变矩阵。

以上讨论中行星是沿着\(z\)轴被压扁的，如果换成任意其他方向\(\vec r\)呢？处理方法是直接的：首先以\(\vec r\)为\(z’\)轴建立新的坐标系，在新的坐标系中写出如上\(T\)和\(C\)，然后将结果变换到原来的坐标系中。这里直接给出结果：行星沿\(\vec r=(x,y,z)^T\)方向受到扁率\(f\)影响时，
\[\begin{aligned}
C(\vec r,f)&=\left(\frac{I}{3}-\frac{\vec r\vec r}{r^2}\right)f\\
&=\left(\frac{1}{3}\begin{pmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}-\frac{1}{x^2+y^2+z^2}\begin{pmatrix}xx & xy & xz\\yx & yy & yz\\zx & zy & zz\end{pmatrix}\right)f
\end{aligned}\]

这就是形变的矩阵表示形式。将第一章的结论写成矩阵形式就是
\[C_\omega=C(\vec \omega,\frac{\omega^2R^3}{2GM})\\
C_m=C(\vec r,-\frac{3GmR^3}{2GMr^3})\]

最后的问题就是不同的形变怎么加起来……一个朴素的想法是，既然球体行星上一点\(P\)在一种形变作用\(C_1\)影响下跑到了\(T_1P\)，那么另一种形变作用\(C_2\)叠加上去应该会让它跑到\(T_2T_1P\)。听起来非常有道理，所以它肯定是正确的（我不会证我们以后会数值验证这个结论）。

所以合形变矩阵为\[\begin{aligned}C&=T_2T_1-I\\&=(I+C_2)(I+C_1)-I\\&=C_1+C_2+C_2C_1\\&\approx C_1+C_2\end{aligned}\]

其中\(C_1C_2\)是高阶小量，略去。

所以结论非常简单~~~对不同的形变\(C_i\)，其叠加即相当于将形变矩阵直接叠加\(C=\sum_i{C_i}\)。形变的效果为将球体行星上的点\(P\)移动到\((I+C)P\)。

再多说两句。矩阵\(C\)是零迹对称矩阵，这个性质在以后的推导中有用。

另外，虽然求单个扁率影响下的\(T\)时保证了行星体积不变，但由于之后过程中省略了一些高阶小量，球体行星经过变换矩阵\((I+C)\)作用后可能有略微的体积改变。为了消除这一改变，可以使用修正的变换矩阵
\[T=\frac{I+C}{[\det(I+C)]^{1/3}}\]

第三章 形变附加势场及其对形变的反影响

啊……终于到这一章了。

之前的计算基于一个假设，行星本身的引力势场仍然是质点势，它与其他影响因素共同确定了行星的等势表面。但实际上形变会改变行星自身势场，而自身势场的改变会进一步作用于行星等势面，产生新的形变，然后无限循环……最终会平衡在某个位置。本章讨论形变引起的附加势，以及考虑这附加势之后的形变平衡位置。

先计算形变附加势。考虑半径为\(R\)的球对称行星，其内部距中心为\(r\)处的密度为\(\rho(r)\)。有给定形变\(C\)作用其上，取行星表面外一点\(\vec r_0\)，则可写出势能
\[\phi(\vec r_0)=-\int_{|\vec r’|\lt R}\frac{G\rho(|\vec r’|)dV’}{|T\vec r’-\vec r_0|}\]

其中\(\vec r’\)是形变前的行星内一点。势能与形变前的差别就在被积量的分母上，\(\vec r’\)跑到了\(T\vec r’\)的位置。由于形变是保证体积与密度不变的，所以质量微元仍然可以写成\(\rho(|\vec r’|)dV’\)。注意到\(C=T-I\)是一个小量，可以做展开：
\[\begin{aligned}
\phi(\vec r_0)=&-G\int\rho(|\vec r’|)dV’\cdot\frac{1}{|\vec r’-\vec r_0+C\vec r’|}\\
=&-G\int\rho(|\vec r’|)dV’\left(\frac{1}{|\vec r’-\vec r_0|}-\frac{\vec r’-\vec r_0}{|\vec r’-\vec r_0|^3}\cdot C\vec r’\right)\\
=&-G\int\frac{\rho(|\vec r’|)dV’}{|\vec r’-\vec r_0|}+G\int\frac{(\vec r’-\vec r_0)\cdot C\vec r’}{|\vec r’-\vec r_0|^3}\rho(|\vec r’|)dV’\\
\end{aligned}\]

注意最后一个式子中的第一项就是原来的球对称行星的引力势，可直接使用牛顿的结论；而第二项中矩阵\(C\)是常量，可以提出来，写成张量双点积的形式：
\[\phi(\vec r_0)=-\frac{GM}{|\vec r_0|}+GC:\int\frac{(\vec r’-\vec r_0)\vec r’}{|\vec r’-\vec r_0|^3}\rho(|\vec r’|)dV’\]
其中\(M=4\pi\int_0^R r^2\rho(r)dr\)是行星的总质量。

定义\(\Delta\phi=\phi+GM/r_0\)是形变造成的附加势，可以看到\(\Delta\phi\)中有一个比较复杂的积分。为了计算这个积分，首先以\(\vec r_0\)为\(z\)轴建立一个新坐标系，在此坐标系中被积函数有轴对称性比较好算。注意，这个积分的结果是张量而非标量，所以在这个坐标系中积完得把结果换回原坐标系，这样才能正确计算和\(C\)的双点积。

在新坐标系中使用球坐标换元，\(dV’=r^2\sin\theta drd\theta d\phi\)，有
\[\vec r_0=(0,0,r_0)^T\\
\vec r’=(r\sin\theta\cos\phi,r\sin\theta\sin\phi,r\cos\theta)^T\\
|\vec r’-\vec r_0|=\sqrt{r^2+r_0^2-2rr_0\cos\theta}\]

以及那个张量，写出来比较吓人
\[
\begin{aligned}
&(\vec r’-\vec r_0)\vec r’=\\&\begin{pmatrix}
r^2\cos^2\phi\sin^2\theta & r^2\cos\phi\sin\phi\sin^2\theta & r^2\cos\phi\cos\theta\sin\theta\\
r^2\cos\phi\sin\phi\sin^2\theta & r^2\sin^2\phi\sin^2\theta & r^2\cos\theta\sin\phi\sin\theta\\
r(r\cos\theta-r_0)\cos\phi\sin\theta & r(r\cos\theta-r_0)\sin\phi\sin\theta & r(r\cos\theta-r_0)\cos\theta
\end{pmatrix}
\end{aligned}
\]

计算原积分，过于详细的过程就不写了（留做习题丢给Mathematica）
\[
\begin{aligned}
&\int\frac{(\vec r’-\vec r_0)\vec r’}{|\vec r’-\vec r_0|^3}\rho(|\vec r’|)dV’\\
=&\int_0^R r^2\rho(r)dr\int_0^\pi \frac{\sin\theta d\theta}{|\vec r’-\vec r_0|^3}\int_0^{2\pi}(\vec r’-\vec r_0)\vec r’d\phi\\
=&\int_0^R r^2\rho(r)dr\int_0^\pi \frac{\pi\sin\theta d\theta}{|\vec r’-\vec r_0|^3}\begin{pmatrix}
r^2\sin^2\theta & 0 & 0\\
0 & r^2\sin^2\theta & 0\\
0 & 0 & 2r(r\cos\theta-r_0)\cos\theta
\end{pmatrix}\\
=&\frac{4\pi}{3r_0^3}\int_0^R r^4\rho(r)dr\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & -2
\end{pmatrix}\\
=&\frac{4\pi}{r_0^3}\left(\frac{I}{3}-\hat z\hat z\right)\int_0^R r^4\rho(r)dr
\end{aligned}
\]

还剩下最后一层积分，仅和行星内部物质密度分布有关，是一个目前无法确定的常数，拥有\(MR^2\)的量纲。定义无量纲量
\[A=\frac{4\pi}{MR^2}\int_0^R r^4\rho(r)dr\]

并且将积分结果变换到原来的坐标系，即有
\[\Delta\phi(\vec r_0)=\frac{AGMR^2}{r_0^3}C:\left(\frac{I}{3}-\frac{\vec r_0\vec r_0}{r_0^2}\right)\]

注意到\(C\)是零迹的（见第二章），故\(C:I=0\)；再用\(\vec r\)代替\(\vec r_0\)重写上式，即为
\[\Delta\phi(\vec r)=-\frac{AGMR^2}{r^5}\vec r\cdot C\vec r\]

这就是形变\(C\)在行星外一点\(\vec r\)处对行星引力势的影响，可以看到这个影响与\(C\)是成正比的。

接下来讨论考虑这一影响之后，行星等势表面应该重新平衡在何处。

继续考虑半径为\(R\)的球体行星。在外部势场\(\phi_{ext}\)作用下，仅考虑其质点势\(\phi_0=-GM/r\)与\(\phi_{ext}\)的平衡，可得行星形变\(C\)，\(C\)的计算在前两章中已经给出。

选择球体行星在未形变时表面上任意两点\(P(\vec r_p),Q(\vec r_q)\)，并假设形变量是小量，形变前后外部势变化不大，可依此写出等势方程：
\[\phi_{ext}(P)-\frac{GM}{|T\vec r_p|}=\phi_{ext}(Q)-\frac{GM}{|T\vec r_q|}\]

移项，展开，化简
\[\begin{aligned}
&\phi_{ext}(P)-\phi_{ext}(Q)\\
=&\frac{GM}{|T\vec r_p|}-\frac{GM}{|T\vec r_q|}\\
=&\frac{GM}{|\vec r_p+C\vec r_p|}-\frac{GM}{|\vec r_q+C\vec r_q|}\\
=&GM\left(\frac{1}{|\vec r_p|}-\frac{\vec r_p}{|\vec r_p|^3}\cdot C\vec r_p\right)-GM\left(\frac{1}{|\vec r_q|}-\frac{\vec r_q}{|\vec r_q|^3}\cdot C\vec r_q\right)\\
=&-\frac{GM}{R^3}\left(\vec r_p\cdot C\vec r_p-\vec r_q\cdot C\vec r_q\right)
\end{aligned}
\]

注意到
\[\begin{aligned}
\Delta\phi(\vec r_p)=&-\frac{AGMR^2}{|\vec r_p|^5}\vec r_p\cdot C\vec r_p\\
=&A\cdot\left(-\frac{GM}{R^3}\vec r_p\cdot C\vec r_p\right)
\end{aligned}\]

而\(\Delta\phi(\vec r_q)\)同理。故上述等势方程可写为
\[\phi_{ext}(P)-\phi_{ext}(Q)=\frac{1}{A}(\Delta\phi(\vec r_p)-\Delta\phi(\vec r_q))\]

假设考虑形变附加势的影响之后，行星形变会平衡在\(kC\)，即原本形变量的\(k\)倍。那么，\(\Delta\phi\)也会变为原本的\(k\)倍。同时等势方程中的\(\phi_{ext}\)也要多出\(\Delta\phi\)的项。依此可以写出新的等势方程：

\[\phi_{ext}(P)+k\Delta\phi(\vec r_p)-(\phi_{ext}(Q)+k\Delta\phi(\vec r_q))=\frac{1}{A}(k\Delta\phi(\vec r_p)-k\Delta\phi(\vec r_q))\]

以上两个等势方程对照，可得
\[\frac{1}{A}+k=\frac{k}{A}\]

解得\(k=1/(1-A)\)。

最后做一总结：行星在因自转、潮汐等作用形变时，可以首先根据前两章公式计算出形变矩阵\(C\)，在此形变下行星的质点势和外部势平衡。但实际中因为形变后的行星自身势场并不是质点势，所以实际形变量是\(kC=C/(1-A)\)，其中：
\[A=\frac{4\pi}{MR^2}\int_0^R r^4\rho(r)dr\\
k=\frac{1}{1-A}\]

形变之后，在行星外一点\(\vec r\)，行星的引力势为
\[\begin{aligned}
\phi(\vec r)=&\phi_0(\vec r)+\Delta\phi(\vec r;kC)\\
=&-\frac{GM}{r}-\frac{AGMR^2}{(1-A)r^5}\vec r\cdot C\vec r\\
=&-GM\left(\frac{1}{r}+\frac{(k-1)R^2}{r^5}\vec r\cdot C\vec r\right)
\end{aligned}\]

间章 一些数值计算

前面一通暴算猛于虎，到底结果精确与否还得拿实际数据检验。这里拿地球的数据算一算。

根据WGS84，地球赤道半径\(a=6378137\mathrm m\)，扁率\(f=1/298.257223563\)，自转角速度\(\omega=72.92115\times 10^{-6} \mathrm{rad/s}\)，重力常数\(GM=3986004.418\times 10^8\mathrm{m^3/s^2}\)。

我们首先假设地球的扁率全是自转引起的，因为第二大的影响是月潮，最高也才米的量级，跟地球扁率导致的几十公里的半径差比起来不值一提。

可以计算地球的平均半径
\[R=(a^2b)^{1/3}=a(1-f)^{1/3}=6371000.79\mathrm m\]

根据第一章的公式，
\[f_\omega=\frac{\omega^2R^3}{2GM}=0.001724893\]

根据第三章的结论，地球最后会平衡到扁率为\(f=kf_\omega\)处，可以计算出\(k\)值
\[k=f/f_\omega=\frac{2GMf}{\omega^2R^3}=1.943779\]

这个\(k\)值是从实测扁率中推出的。然后我们用第三章中的公式理论计算\(k\)值，比较它和实测值的差别，来检验理论的精确性。根据PREM，地球内部的密度曲线可以用一堆间断的多项式来拟合，画出来大概如下图：

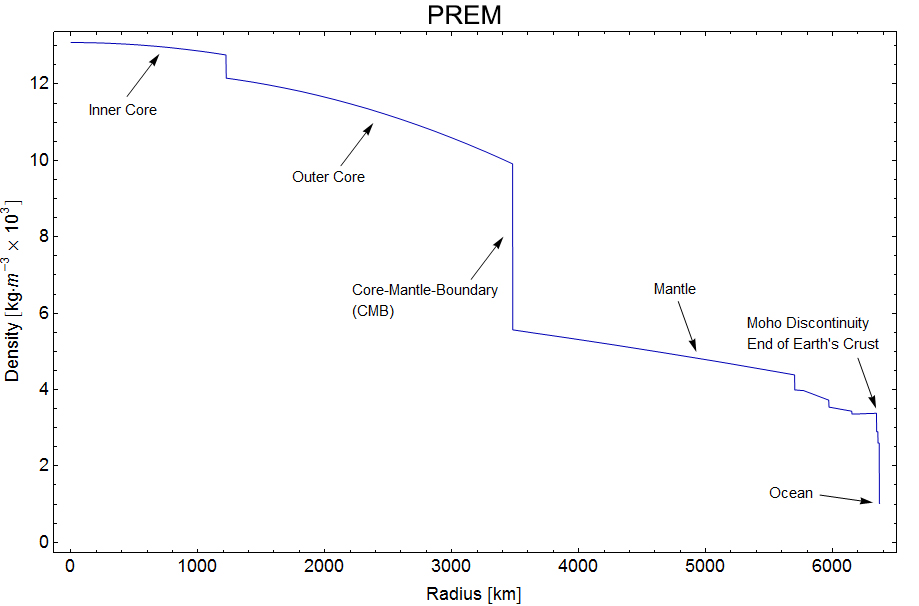
然后数值积分可以算出（过程略）
\[A=\frac{4\pi}{MR^2}\int_0^R r^4\rho(r)dr=0.49620\\
k’=\frac{1}{1-A}=1.98491\]

可以看到计算出的\(k’\)值很接近实际测到的\(k\)值，误差为\(2.116\%\)。反过来就是说如果使用前三章的理论来预测地球的扁率的话，误差只会有\(2.116\%\)，这个精度是令人满意的。至于误差的来源可能是计算过程中舍掉的高阶小量，也可能是因为地球内部并不是处处都根据同一个矩阵\(C\)来形变——可以想象，在更加致密的地球核心区，形变可能稍小。

————————更新（2020.9.2）：对误差的解释：

计算\(\Delta\phi\)时，我们假设了行星的形变矩阵处处为\(C\)，并用行星内部密度的径向分布计算了无量纲量\(A\)。但行星的变形可能并不是在所有半径处都是一致的，所以实际的\(\Delta\phi\)的系数和我们所定义的\(A\)可能有出入，这里用另一个结构常数\(A_r\)表示实际量与定义量的比值。即：
\[\begin{aligned}
k=\frac{1}{1-AA_r}
\end{aligned}\]
根据此修正，地球的\(A=0.49620\)，\(k=1.943779\)，那么\(A_r=0.978513\)。这样就能解释地球扁率和地球内部物质径向分布之间的分歧。需要注意，该解释在此处只是引入了一个参数描述了误差，并没有额外的约束验证该解释的正确性。在本文的第二部分中我们会用地球的进动周期来验证该解释。

另外，由于潮汐的量级一般很小，且时标很短（天体动力时标，比地质时标和自转速率变化的时标短得多），所以行星会对潮汐表现出一定的刚性，并不是百分之百按照潮汐力去变形。故计算潮汐力的形变矩阵时，还需要乘以一个额外的小于\(1\)的经验因子，记为\(k_t\)。地球的\(k_t\approx 0.32\)。描述行星的刚性和物质分布还可以使用另一套叫做Love numbers的参数\(h_2\)和\(k_2\)，它们与本文所用参数的大致关系为\(h_2=kk_t\)，\(k_2=(k-1)k_t\)。

————————更新完毕

最后对\(A,k\)的取值范围做一些分析。首先观察\(A\)的表达式，会发现它其实是\((r/R)^2\)对行星质量的加权平均。在行星几乎所有质量都集中在核心时，\(A\approx 0\)，\(k\approx 1\)；在行星密度均匀分布时，计算得\(A=3/5\)，\(k=5/2\)。那对一般行星自然就有\(1\le k\le 5/2\)，且行星密度分布越集中于核心，\(k\)越接近1；密度分布越均匀，\(k\)越接近\(5/2\)。

根据地球、火星、木星、土星的实测扁率、自转角速度及重力常数，可以计算它们的\(k\)值，如下：地球\(1.94\)，火星\(2.58\)，木星\(1.56\)，土星\(1.38\)。可见土星的物质分布最倾向于集中在核心，而火星完全是个奇葩：要达到大于\(5/2\)的\(k\)值，甚至需要表面密度比核心密度更高！

所以本文的最终结论是：火星的内部是中空的，里面藏着外星人

口胡。无论如何，本文的第一部分就写到这吧，之后会在第二部分中讨论动态形变以及形变引起的其他效果，比如转动惯量变化，天体间额外的力和力矩，潮汐摩擦等等。

第二部分链接